Recta tangente a un círculo en un punto P sobre éste.
- Se llama punto de contacto o tangencia al punto en común entre una circunferencia y la tangente. En geometría la recta tangente es aquella que posee un punto en común con una curva. Una recta y una circunferencia pueden tener dos puntos, un solo punto o ningún punto en común.El punto de intersección es el punto de contacto o el punto de tangencia, como podemos ver es una línea que intercepta al círculo en un punto. Bibliografía.
- Creamos un círculo utilizando la opción 'circunferencia (centro, punto). Debemos poner un punto sobre este círculo, pero al momento de poner definitiva la circunferencia esto nos dejará el punto, el cual es "P".
- Creamos una semi-recta que pase del punto "A" al punto "P".
- Con la opción 'circunferencia (centro, punto)' la colocamos sobre el punto P, esta debe ser pequeña. (verde).
- Marcamos los puntos de intersección de esta nueva circunferencia con la semi-recta. Lo cual nos da el punto "C" y el punto "D".
- De nuevo seleccionamos 'circunferencia (centro, punto)', nos posicionamos sobre el punto C y la abrimos. Repetimos esto pero ahora sobre el punto D. (celeste).
- Marcamos los puntos de intersección de estás dos circunferencias, lo cual nos da los puntos "E" y "F".
- Seleccionamos la opción 'recta' y la creamos de manera que pase por los puntos E y F, al hacerlo, esta recta debe pasar por el punto P.
Recta tangente a un círculo desde un punto P fuera del círculo.
- Se llama punto de contacto o tangencia al punto en común entre una circunferencia y la tangente. En geometría la recta tangente es aquella que posee un punto en común con una curva. Una recta y una circunferencia pueden tener dos puntos, un solo punto o ningún punto en común.El punto de intersección es el punto de contacto o el punto de tangencia, como podemos ver es una línea que intercepta al círculo en un punto.
- Creamos una circunferencia.
- Ponemos un punto fuera de esta en el lugar que sea, se llamará "P".
- Creamos una recta que pase por el punto C y el punto P.
- Creamos una circunferencia, primero damos clic sobre cualquiera de nuestros puntos, ya sea C o P; lo abrimos de manera que sea más grande de la mitad entre el segmento que hay de C a P. Repetimos esto pero ahora damos clic sobre el punto restante y lo abrimos de manera de que esta nueva circunferencia se intersecte con la anterior. (Color gris).
- Marcamos los puntos de intersección entre estas dos circunferencias. Esto nos da los puntos E y F.
- Creamos un segmento que vaya del punto E al F.
- Ponemos un punto en donde este segmento se una con la recta. Este nuevo punto es G.
- Creamos una circunferencia haciendo centro en el punto G y la detenemos sobre el punto C o el P, el que sea está bien. (Rosa).
- Ahora marcamos los puntos de intersección entre esta última circunferencia y nuestro círculo. Serán los puntos H e I (color rosa más fuerte).
- Finalmente solo creamos rectas, una que pase por el punto H hasta P y otra que pase por el punto I hasta P.
Desigualdad del triángulo.
- Desigualdad del triángulo: La suma de las longitudes de cualesquiera dos lados de un triángulo es mayor que la longitud del tercer lado.
- Creamos tres segmentos del tamaño que sea.
- Creamos una recta. Ocultamos los puntos que quedan sobre esta.
- Colocamos un punto sobre la recta (I)
- Seleccionamos la opción compás y después damos clic sobre el segmento más grande, esta circunferencia la colocamos sobre el punto I.
- Ponemos un punto en donde la recta y la circunferencia se intercepten (J).
- De nuevo seleccionamos compás, ahora damos clic sobre uno de los segmentos restantes (yo elegí el mediano), colocamos esta circunferencia sobre el punto J o el punto I, yo lo coloqué sobre el punto J.
- De nuevo seleccionamos compás, damos clic sobre el segmento restante (el más chico) y lo situamos sobre el punto que nos sobra (en mi caso, I).
- La circunferencia que situamos sobre el punto J y la que situamos sobre el punto I deben interceptarse, poner un punto ahí. (K)
- Ahora solo unimos con segmentos del punto J al K y del punto K al punto I.
Ya tenemos el triángulo. Desigualdad del triángulo. Construcción GeoGebra.
Para que se cumpla la desigualdad del triángulo la suma de los lados mas cortos tiene que ser mayor que la medida del lado más grande.
Reconstrucción de un triángulo por el caso ALA.
- ALA: Dos triángulos son congruentes si tienen iguales dos de sus ángulos respectivos y el lado entre ellos.
1.-Hacemos un triángulo.2.-Elegimos la opción compás, damos clic sobre el segmento BC, ponemos esta circunferencia en cualquier parte, ponemos un punto en la circunferencia (E), unimos los dos E y D del círculo con un segmento.3.- Seleccionamos la opción 'circunferencia (centro, punto)' damos clic en el punto B y a continuación damos clic en cualquier parte del segmento BC y marcamos el punto de intersección del segmento AB con esta circunferencia.
4.-Nuevamente seleccionamos la opción compás y damos clic en el punto B, después en el punto F, y al último en el punto E, marcamos el punto de intersección del segmento con esta circunferencia (punto H).5.-Elegimos la opción compás y damos clic sobre el punto F, después sobre el punto G, y al último sobre el punto H, donde se intercepten estas circunferencias ponemos un punto (punto I).6.-Elegimos la opción 'semirrecta' y damos clic sobre el punto E y después sobre el punto I.7.-Elegimos la opción 'circunferencia (centro, punto)' y damos clic sobre el punto C, después damos clic en cualquier parte del segmento BC y marcamos el punto de intersección del segmento AC con la circunferencia.8.-Vamos a la opción compás y damos clic en el punto C, después en el punto J, y luego en el punto D, marcamos el punto de intersección del segmento con la circunferencia, esto nos da el punto L.
9.-De nuevo elegimos la opción compás y damos clic en el punto J, después en el punto K, y luego en el punto L, marcamos el punto donde se intercepten las circunferencias, esto nos da el punto M.
10.-Elegimos la opción semirrecta y damos clic sobre el punto D, después sobre el punto M.11.-Marcar el punto de intersección de las semirrectas.
12.-Damos clic izquierdo sobre una de las semirrectas y damos clic sobre 'objeto visible' y la semirrecta desaparece, repetimos esto con la otra semirrecta.
13.-Seleccionamos la opción 'segmento' y unimos el punto E con el punto N.
14.-De nuevo elegimos segmento y ahora unimos en punto N con el punto D.
Cambié el nombre del punto E a B_1.
El punto D es C_1.
El punto N es A_1.
Para comprobar ponemos las medidas de los ángulos del triángulo y de igual manera la medida de sus lados, las circunferencias pueden ser ocultadas.
Reconstrucción de un triángulo por el casi ALA. Construcción GeoGebra.
Reconstrucción de un triángulo por el caso LAL.
- LAL: Lado, ángulo, lado. Dos triángulos son congruentes si tienen iguales dos de sus lados respectivos y el ángulo comprendido entre ellos.
Inciso a) 5, 90°, 5.
1.-Construimos un segmento con la medida del lado.
2.-Creamos una recta, al crear la recta nos quedarán dos puntos, estos los ocultamos.
3.-Ponemos un punto sobre la recta (E)
4.- Seleccionamos la opción 'compás' y damos clic sobre el segmento y a continuación situamos esta circunferencia sobre el punto E.
5.-Seleccionamos 'circunferencia (centro, punto) y damos clic sobre el punto E. La abrimos cuando queramos, pero que sea pequeña. Nos quedará un punto sobre la circunferencia, lo ocultamos.
6.-Marcamos los puntos de intersección entre esta circunferencia y la recta (puntos G,H).
7.-Ahora volvemos a seleccionar 'circunferencia' pero ahora damos click sobre el punto G y la abrimos, debe ser un poco más grande que la anterior (igual quedará un punto, lo ocultamos). Repetimos esto pero ahora damos clic sobre el punto H y la abrimos, esta circunferencia debe interceptarse con la que creamos recién, marcamos los puntos de intersección, (puntos K,L).
8.-Creamos una recta que pase por los puntos K,L. Esto nos da el ángulo de 90°.
9.-Marcamos los puntos de intersección de esta recta con la primer circunferencia que hicimos, y de igual manera, marcamos el punto de intersección de nuestra primer circunferencia con nuestra primer recta. (Puntos M,N)
10.-Unimos con un segmento el punto M con el N.
Ya tenemos nuestro triángulo de caso LAL.
Reconstrucción de un triángulo por el caso LAL. Construcción GeoGebra
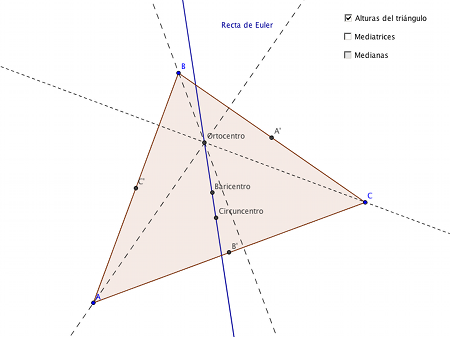
El ortocentro, el baricentro y el circuncentro tienen una curiosa propiedad en común: están alineados.
La recta de Euler de un triángulo es aquella que contiene el ortocentro, el circuncentro y el baricentro del mismo.
Se llama así en honor a Leonhard Euler, ( uno de los grandes de la historia de las Matemáticas), suizo que descubrió este hecho a mediados del siglo XVIII.
Ortocentro/Alturas.
- Ortocentro: Es el punto de corte de las tres alturas.
- Alturas: Altura es cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o su prolongación).
- Creamos un triángulo.
- Utilizamos la opción circunferencia (centro, punto), damos clic sobre cualquier vértice y la abrimos hasta que corte el lado contrario a este vértice, en dos y marcamos los puntos de intersección. Repetimos esta acción con los otros dos vértices y lados. (Si alguna circunferencia no corta en dos al lado, se puede usar una recta auxiliar).
- Creamos un segmento que sea más grande que el que hay entre los dos puntos de intersección.
- Elegimos la opción compás, damos clic sobre el segmento y lo posicionamos sobre uno de los puntos de intersección, repetimos esto pero ahora lo colocamos sobre el otro punto. Repetimos esto con los demás puntos.
- Ponemos puntos en donde estas 2 nuevas circunferencias (azules) se intersectan. Repetimos esto con las demás circunferencias.
- Trazamos rectas por estos puntos.
- Donde estas rectas se unen, es el ortocentro.